Optimization by Julia, 1
Julia
参考文献:
-
Changhyun Kwon, Julia Programming for Operations Research, 2nd Edition, https://www.chkwon.net/julia/
-
https://jump.dev/JuMP.jl/v0.21.1/quickstart/
この書籍で用いられているコードは,上記のwebsiteから入手可能である。テストのために用いられているのは,Julia v1.3.0, JuMP v0.21.2, Optim v0.20.6である。
実行環境
ここでは,Visual Studio Code に 拡張機能としてJulia Languate Supportを導入し,実行する。
@Mizuto_Kadowaki,2020年12月15日に更新,「VSCode で Julia-1.4 を動かすまで」 https://qiita.com/Mizuto_Kadowaki/items/b95e4b7db4a1dfb59863
Juliaでは,最初の要素はv(1)と,添字1でアクセスされる。
Juliaで数理最適化を扱うためのパッケージとして,JuMPがある。 JuMPを用いると,数理最適化問題を簡単に記述することができる。 JuMPのように,人間が簡単に数理最適化問題を記述することができる言語を,モデリング言語という。
JuliaにJuMPをインストールするには,次のようにする。
julia>import Pkg
julia>Pkg.add("JuMP")
例えば,
\[\min \sum_{(i,j) \in A} c_{ij} x_{ij}\]をJuMPを用いて記述すると,
@variable(m, 0<=x[links]<=1)
@objective(m,Min,sum(c[(i,j)]*x[(i,j)] for (i,j) in links))
のように記述することができる。
JuMPは数理最適化問題を記述するだけである。記述した問題を解くには,別にソルバーが必要である。解きたい問題のクラスに対応したソルバーを,Juliaにインストールする必要がある。ここでは,混合整数計画問題を解くためのソルバーとして,Cbcをインストールする。
import Pkg
Pkg.add("Cbc")
using JuMP
using Cbc
最適化問題を定義するには,Model()を用いてモデルを定める。
その際に,用いるソルバーを引数に指定することができる。
julia>model = Model(Cbc.Optimizer)
これを実行すると,次のように表示される。
A JuMP Model
Feasibility problem with:
Variables: 0
Model mode: AUTOMATIC
CachingOptimizer state: EMPTY_OPTIMIZER
Solver name: COIN Branch-and-Cut (Cbc)
このモデルに変数を追加するには,次のようにする。
julia @variable(model,0<=x<=2)
これは,0以上2以下の変数xを,modelに追加するものである。
加えて,変数yも追加する。
julia @variable(model,0<=y<=30)
これらの変数を用いて制約式を追加するには,@constraintを用いて次のようにする。
julia>@constraint(model,con,1x+5y<=3)
これは,$x+5y\leq 3$という制約式を追加するものである。
ここで特徴的なのは,変数の係数を,数値と変数を並べて$5y$などと書くことである。他の言語では,5*xなどと,積を表す記号を入れることが多いが,Juliaでは必要ない。ただし,*を入れた方がわかりやすいのであれば,入れてもよい。
目的関数を定義するには,@objectiveを用いて次のようにする。
julia>@objective(model,Max,5x+3*y)
ここで,2番目の引数Maxは,目的が最大化であることを表す。
こうして定義した最適化問題を解くには,optimzeを用いる。
julia>optimize!(model)
これを実行すると,次のように表示される。
Welcome to the CBC MILP Solver
Version: 2.10.3
Build Date: Nov 9 2020
command line - Cbc_C_Interface -solve -quit (default strategy 1)
Presolve 1 (0) rows, 2 (0) columns and 2 (0) elements
0 Obj -0 Dual inf 28 (2)
1 Obj 15
Optimal - objective value 15
Optimal objective 15 - 1 iterations time 0.002
Total time (CPU seconds): 0.00 (Wallclock seconds): 0.00
この問題は線形計画問題であるが,解いた後の状態は,JuMPの関数であるJuMP.termination_statusで確認することができる。
julia>termination_status(model)
これを実行すると,OPTIMAL:TerminationStatusCode = 1と表示される。このことから,最適解が得られたことがわかる。
得られた最適値は,
julia>objective_value(model)
より15であることがわかる。 また,最適解は,
julia>value(x)
julia>value(y)
より,$(x,y)=(3,0)$であることがわかる。
変数は,ベクトル変数を用いることもできる。例えば,2つの要素x[1],x[2]を一度に定めるには,次のようにする。
julia> model = Model()
julia>@variable(model,x[1:2])
つぎに,3変数の線形計画問題を定義する。
まず,非負変数を定義する。
julia>@variable(model,x[1:3]>=0]
目的関数は
\(\max \sum_{j=1}^3 c_jx_j\) と定められるが,この係数$c_j$を次で定める。
c=[1;2;5]
これらを用いて,目的関数を定義する。
@objective(model,Max,sum(c[i]*x[i] for i in 1:3))
次に,制約条件
\(A x \leq b\) を定義する。ここで,$A$は$m \times n$の行列,$b$は$n$次元のベクトルである。
A=[-1 1 3;1 3 -7]
b=[-5;10]
@constraint(model,constraint1,sum(A[1,i]*x[i] for i in 1:3)<=b[1])
@constraint(model,constraint2,sum(A[2,i]*x[i] for i in 1:3)<=b[2])
こうして定義したmodelをprint(model)で画面表示すると,次のものが表示される。
Max x[1] + 2 x[2] + 5 x[3]
Subject to
constraint1 : -x[1] + x[2] + 3 x[3] ≤ -5.0
constraint2 : x[1] + 3 x[2] - 7 x[3] ≤ 10.0
x[1] ≥ 0.0
x[2] ≥ 0.0
x[3] ≥ 0.0
ここでは制約式の数が2つなのでこの方法で書けたが,100個あるとしたらこの方法で書くことはできない。代わりに,Dict()を用いる。Dict{K,V}()は,型がKのキー,
型がVの値からなるハッシュテーブルを構築する。
キーの比較はisequalで行われる。例えば,次の命令は,文字列をキーとし,整数を値とするテーブルを生成する。
julia>Dict([("A",1),("B",2)])
Dict{String,Int64} with 2 entries:
"B" => 2
"A" => 1
これと同じことは,
julia> c=Dict{String,Int64}()
Dict{String,Int64}()
julia> c["A"]=1
1
julia> c["B"]=2
2
julia> c
Dict{String,Int64} with 2 entries:
"B" => 2
"A" => 1
としても実現できる。
このDict()を用いて,整数をキー,制約式を値とするテーブルを生成すればよい。
julia>constraint=Dict()
julia>for j in 1:2
constraint[j] = @constraint(m,sum(A[j,i]*x[i] for i in 1:3)<=b[j])
end
julia> constraint
Dict{Any,Any} with 2 entries:
2 => x[1] + 3 x[2] - 7 x[3] ≤ 10.0
1 => -x[1] + x[2] + 3 x[3] ≤ -5.0
あるいはもっと簡単に,次のように書くこともできる。
@constraint(model,constraint[j in 1:2],sum(A[j,i]*x[i] for i in 1:3)<=b[j])
変数の範囲を定めるには,boundを用いて例えば次のようにする。
julia>@constraint(m,bound,x[1]<=10)
まとめると次のように書くことができる。
using JuMP, Cbc
m = Model(Cbc.Optimizer)
c=[1;2;5]
A=[-1 1 3;1 3 -7]
b=[-5;10]
@variable(m,x[1:3]>=0)
@objective(m,Max,sum(c[j]*x[j] for j in 1:3))
@constraint(m,constraint[i in 1:2],sum(A[i,j]*x[j] for j in 1:3)<=b[i])
@constraint(m,bound,x[1]<=10)
JuMP.optimize!(m)
println("Optimal solutions:")
for i in 1:3
println("x[$i]=",JuMP.value(x[i]))
end
このプログラムを,LP2.jlという名前のテキストファイルとして保存する。そして,juliaのプロンプト で,
julia>include("LP.jl")
を実行すると,このファイルに書かれた命令が順に実行され,線形計画問題を解いた結果か表示される。
ulia> include("LP2.jl")
Welcome to the CBC MILP Solver
Version: 2.10.3
Build Date: Nov 9 2020
command line - Cbc_C_Interface -solve -quit (default strategy 1)
Presolve 2 (-1) rows, 3 (0) columns and 6 (-1) elements
0 Obj 4.8999999 Primal inf 0.033332367 (1) Dual inf 12.666664 (3)
2 Obj 19.0625
Optimal - objective value 19.0625
After Postsolve, objective 19.0625, infeasibilities - dual 0 (0), primal 0 (0)
Optimal objective 19.0625 - 2 iterations time 0.002, Presolve 0.00
Total time (CPU seconds): 0.00 (Wallclock seconds): 0.00
Optimal solutions:
x[1]=10.0
x[2]=2.1875
x[3]=0.9374999999999999
線形計画問題の変数のうち,いくつかに整数条件が課されたものが,混合整数線形計画問題(mixed integer linear programming)である。 この問題も,JuMPでモデル化することができる。 ここでは,参考文献2から,次の問題例を定式化して解く。
\(\begin{aligned}
\max & x_1 + 2x_2 + 5x_3 \\
\text{s.t.} & -x_1+x_2+3x_3 \leq -5 \\
& x_1 + 3x_2 -7x_3 \leq 10 \\
& 0 \leq x_1 \leq 10 \\
& x_2 \geq 0, \text{integer} \\
& x_3 \in \{0,1\}
\end{aligned}\)
この問題では,変数$x_2,x_3$に整数条件が課されている。
整数の変数を定めるには,@variableの引数に,Intを指定する。0-1変数の場合は,Binを指定する。
julia>@variable(m,0<=x1<=10)
julia>@variable(m,x2>=0,Int)
julia>@variable(m,x3,Bin)
上の問題例を解くためのプログラムは,次の通りである。
using JuMP,Cbc
m=Model(Cbc.Optimizer)
@variable(m,0<=x1<=10)
@variable(m,x2>=0,Int)
@variable(m,x3,Bin)
@objective(m,Max,x1+2x2+5x3)
@constraint(m,constraint1,-x1+x2+3x3<=-5)
@constraint(m,constraint2,x1+3x2-7x3<=10)
print(m)
JuMP.optimize!(m)
println("Optimal Solutions:")
println("x1=",JuMP.value(x1))
println("x2=",JuMP.value(x2))
println("x3=",JuMP.value(x3))
これをMILP1.jlという名前のファイルとして保存し,
julia>include("MILP1.jl")
を実行すると,実行ログが表示された後に,次のように最適解が表示される。
Optimal Solutions:
x1=10.0
x2=2.0
x3=1.0
最小コストネットワークフロー
有向グラフ上の最適化問題を扱う。 有向グラフは,ノード集合$\mathcal{N}$, アーク集合$\mathcal{A}$を用いて, $G=(\mathcal{N},\mathcal{A})$ と定められる。 各アーク$(i,j) \in \mathcal{A}$には,単位量あたりの輸送コスト$c_{ij}$が関連づけられているとする。 各ノード$i \in \mathcal{N}$に,値$b_i$を関連づける。$i$がソースノードであれば,$b_i>0$で,真紅ノードであれば,$b_i<0$となる。どちらでもなければ,$b_i=0$である。ここでは,簡単のために,$\sum_{i \in \mathcal{N}} =0$とするが,これは一般性を失うものではない。
各アークに変数$x_{ij}$を定めるが,これは,$(i,j)$上の流量を表す。流量は非負とする。また,流量には,アークごとに上限$u_{ij}$があるとする。
最小コストフロー問題は,シンクノードでの需要を満たすように,ソースノードから流すフローを定める問題であるが,その際,輸送コストの和を最小するものを求める。 線形計画問題としては,次のように定式化される。
\[\begin{aligned} \min_{x} & \sum_{(i,j) \in \mathcal{A}} c_{ij} x_{ij} \\ \text{s.t.} & \sum_{(i,j) \in \mathcal{A}} x_{ij} - \sum_{(j,i) \in \mathcal{A}} x_{ji} = b_i & \forall i \in \mathcal{N}, \\ & 0 \leq x_{ij} \leq u_{ij} & \forall (i,j) \in \mathcal{A} \end{aligned}\]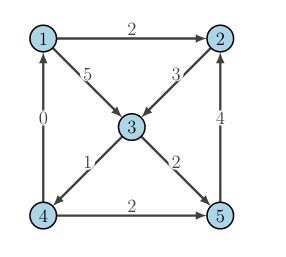
各アークについて,次の表で示される値を持ったネットワーク上での最適化問題をとく。
| 始点 $i$ | 終点 $j$ | $c_{ij}$ | $u_{ij}$ |
|---|---|---|---|
| 1 | 2 | 2 | $\infty$ |
| 1 | 3 | 5 | $\infty$ |
| 2 | 3 | 3 | $\infty$ |
| 3 | 4 | 1 | $\infty$ |
| 3 | 5 | 2 | 1 |
| 4 | 1 | 0 | $\infty$ |
| 4 | 5 | 2 | $\infty$ |
| 5 | 2 | 4 | $\infty$ |
この情報を,csv形式のファイルsimple_network.csvに保存する。
start node i,end node j,c_ij,u_ij
1,2,2,Inf
1,3,5,Inf
2,3,3,Inf
3,4,1,Inf
3,5,2,1
4,1,0,Inf
4,5,2,Inf
5,2,4,Inf
こうして作成したcsvファイルをJuliaで読み込むには,DelimitedFilesのreaddlm()を用いて次のようにする。
using DelimitedFiles
network_data_file="simple_network.csv"
network_data=readdlm(network_data_file,',',header=true)
data=network_data[1]
header=network_data[2]
こうすると,csvファイルの2行目以降のデータが,dataに読み込まれる。
dataを表示すると,次のようになる。
julia> data
8×4 Array{Float64,2}:
1.0 2.0 2.0 Inf
1.0 3.0 5.0 Inf
2.0 3.0 3.0 Inf
3.0 4.0 1.0 Inf
3.0 5.0 2.0 1.0
4.0 1.0 0.0 Inf
4.0 5.0 2.0 Inf
5.0 2.0 4.0 Inf
この1列目をstart_node,2列目をend_node,3列目をc,4列目をu設定する。1列目と2列目は,整数に変換する。
start_node=round.(Int64,data[:,1])
end_node=round.(Int64,data[:,2])
c=data[:,3]
u=data[:,4]
ここで,csvファイルの4列目には,文字列として”Inf”が書かれているが,これらは,Juliaで読み込む際に,無限大を表す数値として変換される。
$b_i$の数値を表すために、もう一つのcsvファイル”simple_network_b.csv”を作成する。
ここでのモデル化では,ノードの総数を数値として用いる。そこで,ノードの添字から,このノードの総数を計算する。今,ネットワークのノードの集合$\mathcal{N}$の要素には,1から順に番号がつけられているとする。このとき,ノードの総数は,start_nodeとend_nodeに含まれる数の最大値としてえられる。また,アークの総数は,start_nodeの長さとしてえられる。
no_node=max(maximum(start_node),maximum(end_node))
no_link=length(start_node)
ここで,maximum()は引数に与えたデータの中での最大値を求めるものである。似た関数に,max()があるが,これは2つの数を比べて大きい方を返すものである。
こうして得たno_nodeとno_linkを用いて,$\mathcal{N}$を表す配列(array)と,$\mathcal{A}$を表すタプルを定める。
julia> links=Tuple((start_node[i],end_node[i]) for i in 1:no_link)
((1, 2), (1, 3), (2, 3), (3, 4), (3, 5), (4, 1), (4, 5), (5, 2))
こうして定めたlinkを用いて,最小コストネットワークフロー問題を定義する。
まず,各アークに対してコスト$c_{ij}$を関連づける。これには,次の命令を用いる。
c_dist=Dict(links.=>c)
u_dist=Dict(links.=>u)
Dict(links.=>c)での=の前に置かれた.は,これが要素ごとの演算であることを表している。テーブルを作成する際に,"a"をキーとし,1を値とするテーブルを作る際に Dict("a"=>1)としたことを思い出すと,このDict(links.=>c)は,linksの各要素を順にキーとし,cの各要素を順に値とするテーブルを生成するものであることがわかる。
この命令を実行してえられるc_dictは,次のようになる。
julia> c_dict
Dict{Tuple{Int64,Int64},Float64} with 8 entries:
(3, 5) => 2.0
(4, 5) => 2.0
(1, 2) => 2.0
(2, 3) => 3.0
(5, 2) => 4.0
(4, 1) => 0.0
(1, 3) => 5.0
(3, 4) => 1.0
これらを用いて,最小コストネットワークフロー問題を定義する。
変数は各アークに対して定義し,それぞれ上限を持つ。
using JuMP,Cbc
mcnf = Model(Cbc.Optimizer)
julia>@variable(mcnf,0<=x[link in links]<=u_dict[link])
julia>@objective(mcnf,Min,sum(c_dict[link]*x[link] for link in links))
julia>for i in nodes
@constraint(mcnf,sum(x[(ii,j)] for (ii,j) in links if ii==i) - sum(x[(j,ii)] for (j,ii) in links if ii==i)==b[i])
end
定義された問題を目で確認するには,print(mcnf)を実行して画面に表示するとよい。
この問題例の最適値は,次の命令を実行することで,45であることがわかる。
julia>JuMP.optimize!(mcnf)
julia>obj=JuMP.objective_value(mcnf)